You want to train a deep neural network. You have the data. It’s labeled and wrangled into a useful format. What do you do now?
When I have a deep learning project, I follow these six steps.
Step 1. Pick a cost function.
Step 2. Pick an initial network architecture.
Step 3. Fit the training set well on the cost function.
Step 4. Fit the validation set well on the cost function.
Step 5. Verify performance on a test set.
Step 6. Verify performance in the real world.
Step 1. Pick a Cost Function
The appropriate cost function depends on the type of problem I’m trying to solve. If I’m predicting an output value given an input value, i.e., a regression problem, I use mean squared error (MSE) loss. If I’m solving a classification problem with more than two classes, use cross-entropy loss. If there are only two classes, I use binary cross-entropy loss. These standard loss functions are available in all major deep learning frameworks.
If I have an unusual problem, such as One-Shot Learning, I may need to design and use a custom loss function.
Step 2. Pick an Initial Network Architecture
For structured learning problems like predicting sales, I’ve found one, fully-connected hidden layer to be a good starting place. The number of activations in that layer should be between the number of input neurons and the number of output neurons. The midpoint between the two usually isn’t a bad choice.
I’ve also seen the following formula, which is fine as a starting point.
\[N_h = \frac{N_s}{(a(N_i + N_o))}\]\(N_i\) = number of input neurons
\(N_o\) = number of output neurons
\(N_s\) = number of samples in the training set
\(a\) = an arbitrary scaling factor between 2 and 10
If I’m doing computer vision, the best place to start is one of the proven architectures like ResNet.
Step 3. Fit the Training Set Well on the Cost Function
The most important hyperparameter in fitting the training set is the learning rate (\(\alpha\)). I don’t bother with trial-and-error and instead use a learning rate finder that I adapted from the fastai library. The learning rate finder outputs a plot that looks like this:
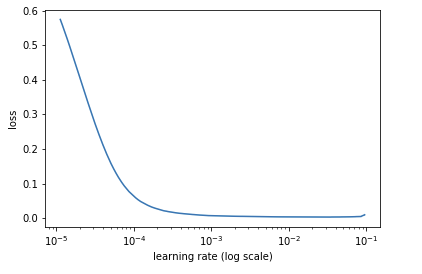
I choose a learning rate where the loss is still clearly decreasing. I tend to pick a point that is a little bit to the right of the steepest point in the plot, i.e., where the loss is still strongly decreasing and has not yet been minimized. In the above plot, I would choose a learning rate of \(10^{-4}\).
If the model is training very slowly or not very well, I replace the initial stochasic gradient descent optimization algorithm with Adam optimization.
If the model still isn’t properly fitting the training set, I’ll add learning rate decay.1 Learning rate decay is reported to have been tried a few different ways: exponential decay, discrete “staircase” decay, and even manual approaches where the experimenter will visually observe when the loss stops decreasing and reduces \(\alpha\) accordingly.
I prefer to use a cosine-shaped learning rate decay, which decays \(\alpha\) over the course of an epoch2 in the shape of a cosine curve. This makes the rate of decay slowest at the beginning and end of the epoch and highest in the middle of the epoch.
I’ll usually also add “restarts” which restarts the learning rate at it’s non-decayed value at the beginning of each epoch (or some integer multiple of epochs).
If I’m using some form of transfer learning, I’ll try unfreezing the earlier layers of the neural network and training it with differential learning rates.
At this point, if I’m still having trouble fitting the training set, I have a few more hyperparameters I’ll tune either sequentially or by random selection in the hyperparameter space.3
- number of units in hidden layer
- minibatch size, in powers of 2: 64, 128, 256, 512. Rarely, 1024.
- number of hidden layers
I don’t bother tuning \(\beta_1\), \(\beta_2\) or \(\epsilon\) for the Adam optimizer, since it doesn’t seem to make much difference.
If, after all this, I still cannot fit the training data well on the cost function, I consider whether the overall objective should be refined. The training inputs simply may not have the right information to predict the output I’m trying to fit.
A good example of this is trying to predict a stock’s future price based solely on that stock’s historical prices. If a stock’s movement is purely a stochastic process as it relates to its historical price, I’m not surprised when I can’t predict it’s future price with a deep neural network.4
Step 4. Fit the Validation Set Well on Cost Function
This is the step where I mainly spend my time. Getting a deep neural network to generalize well to a validation set is often the most difficult part of the project. Your deep neural network at this point almost assuredly performs better on the training set than it does on the validation set. There is in other words at least some degree of overfitting to the training set.
Here are the steps I take to reduce validation set loss.
Dropout
First, I’ll try applying dropout, which randomly zeros-out activations in the training set during training with some probability \(p\). There’s no great rule of thumb for how I set \(p\), but I’ll try a couple of things.
I’ll apply dropout before the last linear layer at \(p = 0.25\) and I’ll run multiple experiments tuning dropout up to \(p = 0.50\). If that doesn’t help, I’ll add dropout to earlier linear layers of the neural network with a similar range of \(p = 0.25\) to \(p = 0.50.\)
Like I said, there isn’t a great rule of thumb here, so it ends up being some experimentation and trial-and-error to determine which combination of dropout probabilities in which layers is the most effective at reducing validation loss.
Weight Decay / L2 Regularization
Second, I’ll add some form of weight decay, such as L2 regularization. This is a classic technique in machine learning that reduces overfitting. It works by adding a term to the cost function that looks like this:
\[\frac{\lambda}{2}\sum_{j=1}^nw_j^2\]\(\lambda\) = regularization hyperparameter
\(w_j\) = feature \(j\) in weight matrix \(w\)
\(n\) = number of features in weight matrix \(w\)
One of the causes of overfitting is large weights, and this form of weight decay heavily penalizes large weights in the weight matrix. By adding this term to the cost function, a gradient step change that increases the size of the weights in the weight matrix must improve the network more than the increased cost associated with larger weights. The weight decay parameter \(\lambda\) is an important one that has to be tuned.
Normalize Inputs
The third thing I’ll do to reduce overfitting is normalize the mean and variance of the input features over the training set. That means the average of input feature \(x_1\) over all training examples \(m\) should equal 0 and the standard deviation should be 1. Same with features \(x_2 ... x_n\).
In math terms, the vector \(x^{(i)}\) containing all of the features \(j\) for a single training example \(i\) should be modified like this:
\[\mu = \frac{1}{m}\sum_{i=1}^mx^{(i)} \\ x := x - \mu\]\(\mu\) is a vector with size equal to the number of input features in a single training example. \(x\) is a matrix of size \(n\) by \(m\), where \(n\) is the number of input features in a single training example and \(m\) is the total number of training examples. The substraction operator in the second equation broadcasts the vector \(\mu\) such that that vector is subtracted from each of the columns of matrix \(x\).
The formula for normalizing the standard deviations should be familiar:
\[\sigma^2 = \frac{1}{m}\sum_{i=1}^m(x^{(i)})^2 \\ x := \frac{x}{\sigma^2}\]I want to reiterate that I normalize the mean and standard deviation for each feature over the training set, not over the features for each sample in the training set. It seems obvious now, but that detail tripped me up initially.
Another important detail is that I keep track of the mean and standard deviation of the inputs from my training set and use those statistics to normalize the validation and test sets. In other words, I don’t calculate a mean and standard deviation over the validation set or test set data. Rather, I use the scaling factors from the training set to scale my validation and test sets.
Batch Normalization
Batch normalization is becoming an increasingly standard part of any deep neural network. Whereas the previous technique normalized the input features, the batch norm technique reduces overfitting by normalizing the mean and variances of the hidden layer activations.
Batch norm is done per-minibatch. Like the input feature normalization, I use the mean and variances from the training set to apply batch norm to the validation and test sets. But unlike input feature normalization, batch norm is done per-minibatch and not over the whole training set, so I actually use an exponentially weighted average of the mean and variances from the training set.
That can be a little mind-bending, so I’ll say it another way. In batch norm, the mean and variance is taken on an activation-by-activation basis over the training samples in the minibatch. Since that will yield as many means and variances as there are minibatches, I then apply an exponentially weighted moving average across the minibatches to obtain a final mean and variance to apply to my validation and test sets.
More Training Data & Data Augmentation
In my experience, overfitting is probably best solved by adding more data to the training set and continuing to train the network. Collecting more data can be expensive and time-consuming, which is why it’s not at the top of my list.
Another approach is to use data augmentation. Data augmentation is the process of synthesizing data to increase the data available to train the network. It is an excellent option in computer vision problems where it can be done by adjusting the lighting, rotation, orientation, or other visual characteristics of the image. In this way, for every image, you could get five or more images from it by transforming it in subtle ways. After all, if you’re trying to build a network that can detect cars on the road, whether that car is oriented left or right, and whether it is sunny or rainy, there is still a car in the photo.
Data augmention as applied to structured data or natural language processing has not really been studied.5
Vanishing and Exploding Gradients
Often, I’ll encounter vanishing gradients or exploding gradients. Vanishing gradients are where where the gradients become so vanishingly small that the network does not learn well with gradient descent. Exploding gradients are where the gradients become so large, they exceed the capability of the computer to calculate.
A first pass at solving both the problem of exploding and vanishing gradients is to initialize the weight matrices in a particular way: so-called, He initialization.
He initialization is characterized by initializing the weight matrix \(W^{[l]}\) to a zero-mean gaussian distribution with a standard deviation of:
\[\sqrt{\frac{2}{l-1}}\]Although I did not expect it, initializing the weights in this particular way has profound effects on minimizing the likelihood of vanishing or exploding gradients.
If I’m training a recurrent neural network for something like language processing, I’ll almost always default to using a Long Short-Term Memory unit in my recurrent neural network, which also operates to reduce the likelihood of vanishing or exploding gradients.
Finally, a couple of notes about exploding gradients specifically. If I start to see NaN appear in my gradients, it’s likely that I have an exploding gradient problem. A blunt but effective way of dealing with exploding gradients is to use gradient clipping. Gradient clipping sets an upper bound on the gradients. If the gradient exceeds a certain threshold, it is “clipped” to the threshold value.
Neural Network Architecture Search
Sometimes, the tuning of these hyperparameters does not seem to make much of a difference. No matter how we tune them, the training set loss is still acceptably low, but the validation set loss is much higher. It therefore often makes sense to take a hard look at the architecture of the neural network. Too many features in the input can cause the network to fit noise in the training set. Too many activations in the hidden layers can do the same thing. So I tinker with the number of neurons in the hidden layers, perhaps reducing them in one hidden layer but increasing them in another hidden layer. Or I will increase or reduce the number of hidden layers themselves.
This technique, like most of the techniques in reducing overfitting, is a lot of trial-and-error. I often need to experiment with many different architectures until I find one that works well.
Step 5. Verify Performance on a Test Set
If the neural network performs well on the training and validation sets, I’m feeling pretty good about it. The main risk at this point is that, in the process of optimizing the network and tuning the hyperparameters, I’ve accidentally overfit my validation set.
When I fit the validation set to the cost function in Step 4, I looked to the loss, F-score or some other optimizing metric with respect to the validation set. In essence, I tuned the hyperparameters specifically optimizing on the validation set. In that way, I may have fit the hyperparameters (and therefore the neural network) to noise in the validation set, and the network may generalize poorly to data it has not yet seen.
So, in this step, I run the network on an as-yet-unseen test set to confirm the same results I saw in the validation set. If the network performs poorly on a test set, I increase the size of the validation set, either by additional data or by data augmentation. I then repeat Step 4 and fit the larger validation before coming back to this Step 5 to verify its performance on a test set.
Don’t tune your network’s hyperparameters with respect to the test set loss! If you do, you’ll end up with a network overfit on your training set, validation set and test set and you won’t realize it.
Step 6. Verify Performance in the Real World
Now the fun part! Make sure the network performs well in the real world. If you’ve trained a cat classifer, start feeding the network pictures of your cat. If you’ve trained a recurrent neural network sentiment classifer for corporate press releases, feed it Microsoft’s latest press releases and see how it does.
If the network performs poorly in the real world, but performs well on the training, validation and test sets, something is wrong. You may have overfit to your test set somehow. Change your validation and test sets and see if the network still performs well on those. If it does, and it still has issues performing in the real world, it may be time to re-evaluate the cost function you are using (or your overall objective).
To be honest, I have not encountered this situation. In my experience, if I successfully make it to this Step 6, the network does not have issues in the real world.
Summary Checklist
Below is a short, checklist summary of the things to do or look out for in each step.
- Step 1. Cost Function
- MSE loss for regression
- Cross-entropy loss for multiclassification
- Binary cross-entropy loss for binary classification
- Step 2. Initial Network Architecture
- Structured learning: one fully-connected layer with number of activations between input output layer sizes.
- Computer vision: start with ResNet.
- Step 3. Training Set
- Choose learning rate with the learning rate finder
- Adam optimization
- Cosine learning rate decay
- Learning rate restarts
- If doing transfer learning, try differential learning rates
- Number of units in hidden layer
- Minibatch size
- Number of hidden layers
- Step 4. Validation Set
- Dropout
- L2 regularization
- Normalize input features
- Batch normalization
- Data augmentation
- Obtain additional training set data
- Vanishing / exploding gradients
- He initialization
- Use Long Short-Term Memory units
- Gradient clipping
- Revisit the architecture of the neural network
- Step 5. Test Set
- If there are issues, increase size of validation set and go back to Step 4.
- Step 6. Real World
- If issues, change validation and test sets and go back to step 4.
Acknowledgements
This post is inspired by my experiences in the deeplearning.ai Coursera specialization as well as the Practical Deep Learning for Coders course. Many thanks to Andrew Ng and Jeremy Howard for their hard work as educators.
Footnotes
-
This learning rate decay is in addition to the effective decay that is part of the Adam optimizer. ↩
-
An epoch is a single full pass through all the training data. It is comprised of minibatches. ↩
-
If I’m tuning multiple hyperparameters at once, I avoid grid searches in the hyperparameter space in favor of random selection. ↩
-
If you think you have, you’ve almost certainly just fit noise / overfit on the the training set. ↩
-
I am currently studying the potential for financial data augmentation using synthetic financial data. To date, synthetic financial data has been used to improve backtesting by using historical information to generate a dataset with statistical characteristics similar to the observed data. I’m hopeful that the same principles will lend themselves well to augmentation of training data. ↩